UCM解析

その8：変動を2つに分けて大きさを求める

Y田研究員：次は、結果に影響するバラツキの大きさと、結果に影響しないバラツキの大きさを計算して比較する方法だね。

S銀研究員：はい。

Y：全体のバラツキの大きさを求める前に、1回の変動の大きさを分解する作業をやってみよう。まず、目標とする二人の音量の合計である赤い直線に対して、直交する方向と平行な方向とを考えてみよう。そうしてみると、平行方向ではどう動いても合計の音量は変わらない。これに対して直交方向ではその動きによって直接、合計の音量が変化する。

S：平行方向と直交方向ですか・・・赤い直線に対してだから、こっちとこっちの方向になりますよね？（グラフに書き込んでみる）

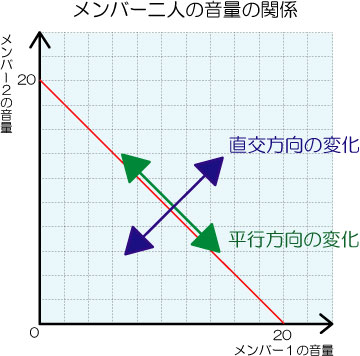
Y：そうだね。この図でいうと、緑色方向の成分と青色方向の成分の比率が大事なんだ。それぞれの成分の大きさを比較して、どちらの広がりが大きいか？　「見た感じ」だけだと、定量的な評価にはならない。

S：確かに。じゃあ、これを計算的に表現するんですね。

Y：そう、数値的、数学的にね。この方向ごとに、前回話したような分散を求めて比較するんだ。赤い直線（等音量線）に平行な方向（緑）は合計音量を保つ際には制御を受ける必要がないので、Uncontrolled Manifold、UCM方向と呼んでいるみたい。UCMに直交する方向（青）は、直交を英語ではOrthogonalというので、ORT方向と呼ぶことが多いかな。

S：！！！・・・ついに出た！そいつが待ちに待ったゆーしーえむですね！？

Y：まだまだ。焦らないで。これからまた少し難しい計算の話に入っていくよ。それじゃあ、ORT方向の分散とUCM方向の分散をどう求めたらいいかわかるかな？

S：えーと・・・一次元量の分散はああやって求めて、二次元量の分散はこうやって求めるから、この場合は一次元量だけど軸が傾いてるから・・・と、うーん（汗）。

Y：もう少し詳しく書いて説明していこう。今回の例では、二人の音量をそれぞれx、yにとったグラフにおいて、同じ音量になる直線（等音量線）の傾きは(-1)だよね。

Y：図に戻って具体例で考えてみよう。例えばa（8,12）という点があって、b（12,10）という点に移動したとする。

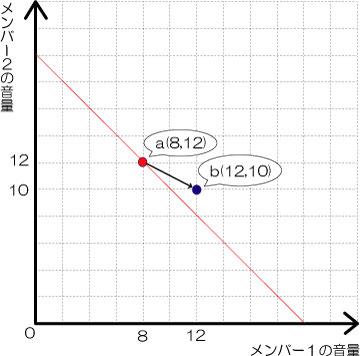
Y：図を見てもわかるとおり、aからbへの移動は、メンバー1の音量はx方向に＋4、メンバー2の音量はy方向に-2だけ移動したことになるよね。このとき、ORT方向とUCM方向にどれだけ移動したかはどうやって求めたらいいかわかるかな？

S：えーと・・・軸が傾いているから・・・うーん？

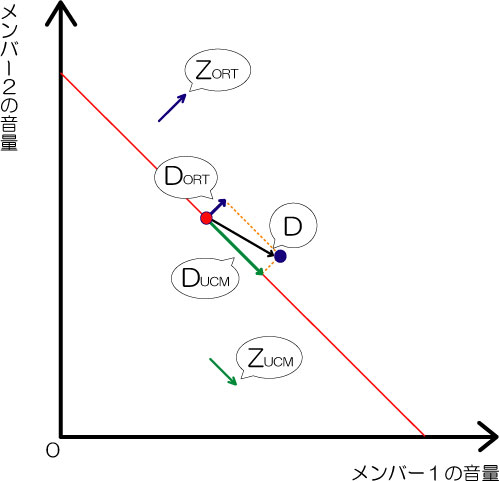
Y：a点からb点に向かうベクトルを　D とおくと D　=　(4, -2)。 このベクトルのUCM方向の成分とORT方向の成分を求めればいいわけ。そのために、まずはUCM方向とORT方向の単位ベクトル　Z_UCM　と　Z_ORT　を求めてみよう。

S：単位ベクトル・・・それならば、傾きが（-1）、つまり45度傾いているんだから、　Z_UCM =　（1/√2, -1/√2）、　ORT方向は　Z_ORT =　（1/√2, 1/√2）ですね。

Y：そうだね。一応、念のために確認しておこう。

　赤線で書いた「等音量線」は傾き（-1）の直線。xが1増えたらyは(-1)増える。ということは、ベクトル(1, -1)の方向はこの直線の方向と同じ。このベクトルの大きさは√{1 ²+(-1) ²} = √2なので、このベクトルを√2で割れば「等音量線と平行で大きさ１のベクトル」つまり「UCMの方向の単位ベクトル」になる。というわけで、Z_UCM = （1/√2, -1/√2）。

　続いて、Z_ORT =（1/√2, 1/√2）が正しいかどうかは、これが　Z_UCM　と直交する単位ベクトルであることを示せば良い。2つのベクトルが直交するときは両者の内積はゼロになる。確かめてみると、（1/√2, -1/√2）・（1/√2, 1/√2）= 1/2 - 1/2 = 0 となって、見事に直交。さらにベクトルの大きさは、√{(1/√2) ²+(1/√2) ²} = 1となって、こちらもOK。

S：安心しました。

Y：安心するのは、ちょっと早いかも。

S：えっ？

Y：このまま計算に進んでも、全く問題は起こらないんだけど、ちょっとだけ押さえておきたい点があるんですよ。確かに、（1/√2, -1/√2）と（1/√2, 1/√2）は　Z_UCM　と　Z_ORT　の条件を満たしているけど、これだけが唯一の正解と言っていいんだろうか？（...と不敵に微笑む）

S：うっ、それは明らかに他にも答えがある、ということでは？（...とたじろぐ）

Y：さっき、「45度傾いている」って言ったでしょ？　何が、何に対して、どっちから計って45度傾いているの？　（...とたたみ込む）

S：何が、何に対して、どっちから？？
え〜と、そうか！　どっちからって、この際、方向は関係ないわけですね。平行か、直交か、という点だけが重要。

Y：そうそう。そうすると？

S：Z_UCM　は（1/√2, -1/√2）だけでなく、方向を逆にした（-1/√2, 1/√2）でもいい。同じように、　Z_ORT は（1/√2, 1/√2）でもいいけど、逆方向の（-1/√2, -1/√2）でもいい！

Y：そういうわけです。計算結果はどっちを使っても同じになるし、この例では計算のしやすさもどっちも変わらない。でも、別の例を考えるようなときには、計算のしやすさとか式の見やすさが変わることもあるかもしれないから、ベクトルの向きの関係は意識しておくと役立つかもね。

S：了解です。

Y：さて話をもどして、a点からb点に向かうベクトルはD　=　(4, -2)。　DのUCM方向の成分D_UCMは DとZ_UCMのスカラ積（内積）から求まるし、 DのORT方向の成分D_ORTはDとZ_ORTのスカラ積から求まる。

S: スカラ積！昔やったような気がします（笑）。

S: ちょっと待ってくださいよ。えーと...

D_UCM　= D ･ Z_UCM
　　　　　= (4, -2) ･ (1/√2, -1/√2)
　　　　　= { 4 × 1/√2 + (-2） × （-1/√2） }
　　　　　= 6/√2
　　　　　= 3√2

D_ORT　= D ･ Z_ORT
　　　　　= (4, -2) ･ (1/√2, 1/√2)
　　　　　= { 4 × 1/√2 + (-2） × 1/√2 }
　　　　　= 2/√2
　　　　　= √2

　...でしょうか。

Y: そうなるかな。じゃあ、念のため検算してみて。D の大きさを、D_UCM　と　D_ORT　から求めたものと、各メンバーの音量の変動から求めたものとで比べてみるのが手っ取り早いかな。

S: D の大きさを求めるということは、ピタゴラスの定理に当てはめて、D の大きさの二乗が　D_UCM　の二乗と　D_ORT　の二乗とを加えたものに等しいので、と。

|D|² = (D_UCM ) ² + (D_ORT ) ²
|D| = √{ (D_UCM ) ² + (D_ORT ) ² }
　　= √{ (3√2)² + (√2)² }
　　= √( 18 + 2 )
　　= √20

　で、次は、各メンバーの音量の変動から求めてみると、a（8,12）からb（12,10）に移動したので、その差をとって、D　=　(4, -2)　だったから、同じくピタゴラスの定理に当てはめてみて、と・・・

|D| = √{ (4)² + (-2)² }
　　= √( 16 + 4 )
　　= √20

　...両方とも√20になりました。

Y：ちゃんと同じになって良かったね。というわけで、こんな感じで移動量や変化量のUCM方向とORT方向の成分を求めることができるわけだ。ここまでで、３つの量を数値化したことになる。１つは点aから点bへの変化を表すベクトル D の大きさ。これが√20。あとの二つは D を分解した成分D_UCM = 3√2 と D_ORT = √2。これらの数値の意味はわかる？

S：意味...ですか？

Y：そう。数値化してみたのは、その数値から協調性を見るためなんだけど、...ここからまた少し長くなりそうなので、以下、次号！

---

その7:結果に影響するﾊﾞﾗﾂｷと影響しないﾊﾞﾗﾂｷ ｜生体工学技術へ｜その9:ﾊﾞﾗﾂｷを2つに分けて大きさを比べる

---