UCM解析

その12：一般化：　メンバーが3人以上のときはどうなるの？

S銀研究員：　えーと、今回は目標値が変動する場合の話でしたよね。なんだか記憶が曖昧で。

Y田研究員：　私も不思議と前回が遠い昔のような気がして、前回の分を読み返してみたんだけど、冒頭のあたりをみると元々の流れは別の方向だったみたい。

S：　と言うと？

Y：　最初はグラフを使って、「位相面」とか「状態空間」のなかでの点、つまりデータ、のバラツキの形から協調性があるとか無いとかの説明をしてきたよね。

S：　それに対して、前回はグラフが一個も出てこなかったですね。やたらと数式ばっかりで。なんでしたっけ、トレビアンとかいう...

Y：　ヤコビアンだってば。要素が２個かせいぜい３個のときまでは、グラフでイメージを掴むことができたけど、要素数がそれ以上のときはグラフは使えない。

S：　なるほど、４次元のグラフを描けっていわれても困りますよね。　

Y：　なので、どうしても数式を使わざるを得ない。実際に何か実験結果を解析するときも、数式で計算できないとどうしようもないしね。そこで、前回はそのための準備をしてたわけですよ。

S：　じゃあ、今回はメンバーが増えたときの話にするわけですね。

Y：　そういうこと。まずはちょっと、メンバーが3人になったときを考えてみたい。3人だったらギリギリ三次元の図に描くことができる。なので、3次元の図を使いながら、今までのメンバー2人だったときの話を3人に拡張して話してみたい。2人から3人への拡張が成功すれば、あとは任意の人数での協調性の解析もできるようになる。

S：了解です。

Y：じゃあ、3人の場合で、音量のグラフを作ってもらってもいい？　（紙に描きながら）こんな感じのグラフをパワーポイントで作ってみて。これまでのと色を合わせてね。

S：はいはい。(ちょいちょい、っと)

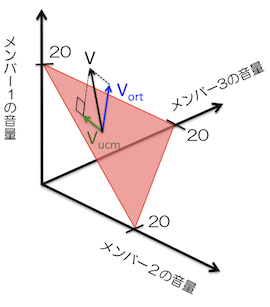
Y：今までは、「等音量線」みたいなものを２次元のグラフの中の赤い「線」で書いてきたよね。右下がりの直線。今度はメンバーが３人なので、グラフは３次元のグラフになって、赤い「線」の代わりに赤い「面」が出てきた。この太鼓の音量の例では、この面上の点ならどこでも「合計音量20」になってる。わかる？

S：えっと、少しずつ考えてゆきましょう。例えば、メンバー1,2,3のそれぞれの音量が5,5,10のとき、これはxyzグラフ上の(5, 5, 10）位置の点で表現できるわけですよね

Y：そうそう。そこから一般化してゆきましょう。

S：メンバー1,2,3のそれぞれの音量をx,y,zとすると、それはグラフの点(x,y,z)に対応するわけで、今の場合は合計音量が20なんだから、x+y+z = 20、の関係があるわけで...

Y：それ(x+y+z = 20)が結局、３次元での平面の方程式になってるわけだよね。x,y,zの係数が(1,1,1）だからベクトル(1,1,1）と直交する平面。

S：なるほど。「等音量面」つまり、３次元でのUCM空間は平面になるわけですね。

Y：いやいや、今回の例では確かに「平面」だけど、一般には平面とは限らないよ。曲面の場合なんかもあり得る。
　さて、等音量面が用意できたので、音の変動を、この面に平行な成分と直行する成分に分けて考えることができるわけ。

S：今度は面の平行、直行成分ですか。

Y：そう。各メンバーの変動をベクトルにすると、３次元グラフの赤い面上の黒い矢印（ベクトルＶ）みたいな形式で描けるわけ。

S：Ｖを赤い面に投影したのが緑のVcumで、赤い面に直交するのがＶortですね。ortはそもそも「直交の」のorthogonalですもんね。

Y：図で描くとそういうこと。この図は１回叩いた時の変動をイメージしているけど、何回も叩いた時の分散を式に起こしてみましょう。全体の変動Vtotはどんな式で計算できる？

S：おっと。式ですか。

Y：分散の計算には平均が必要だから、平均の記号を決めとこうか。今まではm1の平均をm1_mとか書いていたけど、メンバー(manber)のmと平均(mean)のmがカブっていて、式が複雑になってくるとちょっとわかりにくい。平均を表すのにＥ(expectation）も良く使われるので、x(1), x(2), ..., x(n)の平均をE(x)と書くことにしようか。ちゃんと書くと、$Ｅ(x) = \frac{1}{n} \sum_{i=1}^{n}x(i)$ということ。

S：えーと、m1とm2の2人のとき（その6）は \[ \begin{align} V_{tot} = \frac{1}{n} \sum_{i=1}^n\left\{ (m_{1}(i)-E(m_{1}))^2+ (m_{2}(i)-E(m_{2}))^2\right\} \label{eq:a} \end{align} \] これを3人に増やして、と・・・

\[ \begin{align} V_{tot} = \frac{1}{n} \sum_{i=1}^n \left\{ (m_{1}(i)-E(m_{1}))^2+(m_{2}(i)-E(m_{2}))^2)+(m_{3}(i)-E(m_{3}))^2 \right\} \label{eq:b} \end{align} \]

Y：今後のために、それが3人でなくてk人になっても対応できるほうが良いね。k人だったらどんな式になるでしょうか？

S：k人ですか？　そうすると、メンバー番号をjとしてΣでまとめると、こんな感じになりますでしょうか。

\[ \begin{align} V_{tot} = \frac{1}{n} \sum_{i=1}^n \left\{ \sum_{j=1}^k (m_{j}(i) - E(m_{j}) )^2 \right\} \label{eq:c} \end{align} \]

Y：そうだね。全体の変動はこんな風に簡単に拡張できる。これを、UCM方向と、ORT方向に分解しなければいけない。では、どんな風にしたら分解できるでしょうか？

S：う。連発ですね。えーと・・・わからんです。

Y：基本的な考え方としては、UCM方向の単位ベクトルと、ORT方向の単位ベクトルを使って変動を分解してあげればよい。念のために、メンバー2人のときの分解の式を書いてもらえる？

S：そしたら、全メンバーのプレイの変動をΔPとおくと。１回叩いたとき、平均からどれくらいズレたか、っていう値、とうかベクトルですね。メンバーiの音量miの変動をΔmiと書けば、それらをならべたベクトル(Δm1, Δm2, ..., Δmk)がΔPですね。このベクトルがUCM成分とORT成分に分けられますよ、というのを式で書けば、 \[ \begin{align} {\Delta P = \Delta P_{UCM} + \Delta P_{ORT}} \label{eq:d} \end{align} \] ΔPのUCM成分の大きさは、UCM方向の単位ベクトル e_ucmとの内積をとれば求まるので、結局、 \[ \begin{align} {\Delta P_{UCM} = (\boldsymbol{e}_{UCM} \cdot \Delta P) \boldsymbol{e}_{UCM}} \label{eq:e} \end{align} \] 同様にORT成分は、 \[ \begin{align} {\Delta P_{ORT} = (\boldsymbol{e}_{ORT} \cdot \Delta P) \boldsymbol{e}_{ORT}} \label{eq:f} \end{align} \] これは1回叩いたときの変動の大きさなので、分散はこれの二乗平均で計算できるから、 \[ \begin{align} V_{UCM} = \frac{1}{n} \cdot \sum \left\{ \Delta P_{UCM}(i) \right\} ^2 \label{eq:g} \end{align} \] \[ \begin{align} V_{ORT} = \frac{1}{n} \cdot \sum \left\{ \Delta P_{ORT}(i) \right\} ^2 \label{eq:h} \end{align} \]

Y：二次元版のときにはこうやって分解することができました。じゃあ、これを三次元版に拡張したらどうなるでしょう？

S：うーん・・・変わらない？

Y：ちゃんと言うと、変わらない部分と変わる部分がある。ベクトルの計算式にしておけば、式\eqref{eq:c}については変わらない。でもね、式\eqref{eq:d}以降については問題がある。メンバー3人のときはこうは行かないんですよ。
メンバーが２人のときは次の式\eqref{eq:i}みたいに書けるんだけど、３人以上のときでもこれで良いのかな？

\[ \begin{align} {\Delta P = K_{UCM} \boldsymbol{e}_{UCM} + K_{ORT} \boldsymbol{e}_{ORT}} 　（3自由度以上の場合は誤）\label{eq:i} \end{align} \]

S：ん？

Y：だめ。さっきのグラフに戻って考えると、ΔPを分解したときのΔP_ORT は1次元でいいけど、 ΔP_UCM は2次元になる。なので、そのままだとだめ。基底を考えるとこの辺はアドバンスドで難しいんだけど、式\eqref{eq:j}のようにならないといけない。 \[ \begin{align} {\Delta P = K^{(1)}_{UCM} \boldsymbol{e}^{(1)}_{UCM} + K^{(2)}_{UCM} \boldsymbol{e}^{(2)}_{UCM} + K_{ORT} \boldsymbol{e}_{ORT}} \label{eq:j} \end{align} \] プレイヤー３人の場合、UCMは２次元。図では等音量「面」。２次元ということは基底ベクトルeが２つ必要になる。上の式ではそれを$\boldsymbol{e}^{(1)}_{UCM}$と$\boldsymbol{e}^{(2)}_{UCM} $で示している。で、ORT方向の単位ベクトル$\boldsymbol{e}_{ORT}$はどう求めようか？

S：UCM平面内のベクトルを2つ作って、それに直行するベクトルを求めようかと思いましたが。

Y：それでできないこともないけれど、ちょっと面倒になる。というのも、UCMの2次元平面を決める基底ベクトルが一意に決まらないので面倒くさい。それに対して、ORT方向のベクトルは一意に決まるので、こちらから求めていくとだいぶ楽になる。
　じゃあ、それをどうやって求めたらいいでしょう？

S：わかりません。

Y：それはすごく難しいんだけど、まずは、全プレイヤーの音量のベクトルPと全体の音量（音量の合計）の関係を定式化しておきたいと思う。Pは各プレーヤーの音量mを要素にもつベクトルなので、 \[ \begin{align} {\boldsymbol{P} =( m_{1} , m_{2}, \ \cdots,\ m_{k})} \label{eq:j2} \end{align} \] 　それから、全体の音量をSと書くとこれは単純に全メンバーの音量の和なので、 \[ \begin{align} {S = m_{1} + m_{2} \ +,\ \cdots,\ + m_{k}} \label{eq:k} \end{align} \] 　このPとSの関係って、内積を使うとこんな式で書けちゃう。 \[ \begin{align} {S = (1, \ 1,\ \ldots ,\ 1) \cdot \boldsymbol{P}} \label{eq:l} \end{align} \] 　そうすると、全体音量の変動ΔSと各メンバーの変動のベクトルΔPは、同じ形式になります。 \[ \begin{align} {\Delta S = (1,\ 1,\ ... ,\ 1) \cdot \Delta{\boldsymbol{P}}} \label{eq:m} \end{align} \] 　実はこの頭にでてきてる(１, １, ..., １)というベクトル、これがヤコビアンと呼ばれるベクトルで、この方向こそがORTの方向を表しているんです。

S：出た、ヤコビアン！　前回（その11）やったこの式とほとんど同じですね。
\[ \begin{align} {\Delta S = (1,\ 1) \cdot (\Delta P_{1}, \Delta P_{2})} \label{eq:m2} \end{align} \]

Y：そう...なんだけど、よく見たら記号が不統一だね。この式、つまり、前回の説明のP1,P2は、上の方のm1,m2と同じだね。plyerのpとmemberのmがどっかから混在したのかな。まあ、なんとかわかるかな。
　いずれにせよ、前回わざわざヤコビアンを使ったことが活きてくるわけ。この方向こそがORTの方向なので、この単位ベクトルを求めれば、それがe_ORT 。e_ORT が求まれば、\eqref{eq:d}式を使って、 ΔP_ORT が求まる。ΔPと ΔP_ORT が求まってしまえば、実はΔP_UCM は簡単に求まってしまうんだけど、どうしたらよいと思う？

S：式\eqref{eq:d}？

Y：そうそう、変形してΔP_UCMについて解いてやればいい。具体的には、 \[ \begin{align} {\Delta P_{UCM} = \Delta P - \Delta P_{ORT} } \label{eq:n} \end{align} \] となるので、これがあれば、式\eqref{eq:g}に代入してV_UCM が求まる。 ΔP_ORT も求まっているので、V_ORTも求まる。さっき求めたV_totもΔPを使っておくと、\eqref{eq:o}式のようになる。 \[ \begin{align} {V_{tot} = \frac{1}{n} \cdot \sum \left\{ \Delta P(i) \right\} ^2} \label{eq:o} \end{align} \] Y：そうすると、V_tot、V_UCM 、V_ORTが出揃ったので、今までと同じように、ΔVを求めることができる。さて、どんな式になるでしょう？

S：（カキカキ...） \[ \begin{align} {\Delta V = ( V_{UCM} - V_{ORT}) / V_{tot} } 　（3自由度以上の場合は誤）\label{eq:q} \end{align} \]

Y：そう書きたくなるだろうけど、３次元以上の場合にはちょっと注意しないといけないところがある。

S：と言いますと？

Y：UCMの空間とORTの空間では、広さが違う。

S：広さ...ですか？

Y：正確に言うと、次元の大きさが違う。2次元で協調性がないケースをグラフで描くとどんな風になったっけ？

S：円形に散らばってましたね。

Y：そのとおり。では3次元版では、協調性がないケースではバラツキのグラフはどんな形になる？

S：２次元で円なら、３次元だと球になる？

Y：そういうこと。ここで考えて欲しいのは、各要素がランダムにばらつくつと３次元の球になるんだけど、そのうちORT方向のバラツキは１次元分、UCM方向のバラツキは２次元分だということ。

S：うーん？もうちょっと詳しく教えて下さい。

Y：さっきのグラフの「等音量面」をイメージしてみて。あの面に平行な面については、面の上のどの点でも同じ合計音量になる。

S：等音量面に平行な動き、つまりバラツキについては合計音量に影響ないので、これがUCMの方向。「面」だから２次元。UCM方向は２次元。ということですね。ORTは残りの１次元。

Y：そうなるとね、ランダムにばらついたとしてもUCM方向のバラツキはORT方向のバラツキより大きくなるわけ。UCMは平面内がバラツキの範囲だけど、ORTは面から離れるか近づくかという距離方向にバラつくことしかできない。

S：ふむふむ。

Y：結局ね、式\eqref{eq:q}で、 V_UCM から V_ORTをそのまま引き算するとフェアじゃない。

S：じゃあ、どうすれば良いんですか？

Y：１自由度あたりの分散の比較をするのが順当じゃないかな。つまり、V_UCMは２次元だから２で割る。V_ORTは１次元だから、丁寧に書くなら１で割る。結局、式\eqref{eq:q}の右辺の分子は、( V_UCM /2 - V_ORT/1）。

S：そうすると、式\eqref{eq:q}の代わりに、 \[ \begin{align} {\Delta V = \left( \frac{V_{UCM}}{2} - \frac{V_{ORT}}{1}\right) / V_{tot} }　\label{eq:r}　 　　（誤） \end{align} \] 　となれば良いわけですね。

Y：惜しい。V_UCMも V_ORT も１自由度あたりの分散で比較しているので、 ここではV_totも１自由度あたりの値にしておこう。

S：そういうことなら、V_totは３次元なので、

\[ \begin{align} {\Delta V = \left( \frac{V_{UCM}}{2} - \frac{V_{ORT}}{1}\right) / \left( \frac{V_{tot}}{3} \right) } \label{eq:s} \end{align} \]

　ならどうですか。

Y：そのとおり。一般には、こんなふうに自由度数で正規化した分散の比較からΔVを計算することが多いみたい。ところで、２次元のΔVを式\eqref{eq:q}で計算したときの最大値、つまり最も協調性が高い場合の数値は、いくつだったっけ？

S：えーと、分散全体がV_UCM方向になって、V_ORT はゼロで、この時は結局、V_UCMはV_totそのものになるので、

\[ \begin{eqnarray} \Delta V &=& ( V_{UCM} - V_{ORT}) / V_{tot} \nonumber\\ &=& ( V_{UCM} - 0) / V_{UCM} \nonumber\\ &=& 1　\label{eq:t} \end{eqnarray} \]

S：ということで、ΔVの最大値は１でしたね（その10） 。

Y：そのとおり。だけど、式\eqref{eq:s}では最大値は１になるかな？

S：そんな言い方をするってことは、ならないんですよね。ええと同じ流儀で、 V_ORT = 0、 V_UCM = V_totの関係を式\eqref{eq:s}に代入すると、 \[ \begin{eqnarray} \Delta V &= &\left( \frac{V_{UCM}}{2} - \frac{V_{ORT}}{1} \right) / \frac{V_{tot}}{3} \nonumber\\ &=& \left( \frac{V_{UCM}}{2} - 0 \right) / \frac{V_{UCM}}{3} \nonumber\\ &=& 1.5　\label{eq:u} \end{eqnarray} \] 　おお、いつも最大が１というわけではないんですね！

Y：そうなんです。そのあたりには気をつけないといけないのだけれど、ここまでたどり着けば、あとは４次元でも10次元でも同じように計算ができるというわけ。

S：ふむふむ。

Y：だいたいこんな感じで終了かな。

S：あの、目標値が変動する場合の話が残ってましたよね。

Y：しっ。黙ってればだれも気がつかないから。

---

その11：これまでのまとめと、一般化への拡張の準備 　　　｜　　　生体工学技術へ　　　｜　　　その13：一般化：　目標値が変動するときはどうなるの？

---